No investment crystal ball needed

Realistically estimating strategy performance through stochastic models.

Money managers have a tough job. They need to raise capital, build and maintain client relationships, keep in compliance of regulations, and then actually manage investments. All of these areas of practice are important and interrelated, and any one of them can be disastrous when not managed properly. The foundation of managing the practice well often boils down to properly setting expectations with clients and then meeting them. One of the most important expectations centers on meeting clients’ goals that depend on future investment risk-return performance.

Setting expectations on future performance is an inherently difficult thing to do. It is much easier (and often required for compliance) to make a statement such as “past performance is no guarantee of future results.” Yet people naturally focus on past performance. However, financial markets are extremely complex systems, and a singular historical path is insufficient to predict future outcomes. Future performance is unknown. Instead of projecting, investors should think in terms of probabilities and statistical distributions.

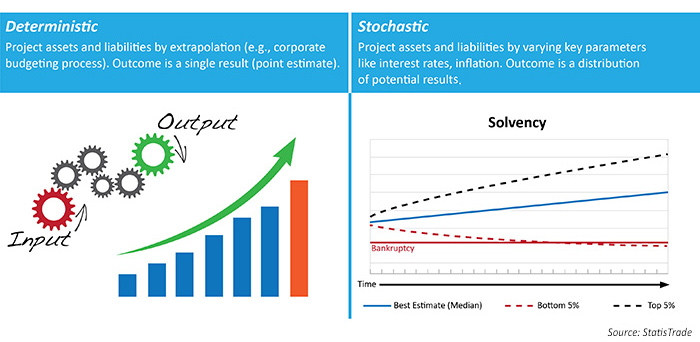
Insurance companies figured this out long ago. Like any business, in order to remain solvent, future assets need to exceed future liabilities. The problem is that both depend on complex factors across hundreds or thousands of policies, guarantees, and investments, all of which are unknown. In the days before powerful computers and data centers were ubiquitous, actuaries would project assets and liabilities by extrapolating from past performance. The problem with this approach is that it does not allow for the volatility of investment returns in each future time period or the chance that an extreme event in a particular time period leads to an investment return that is less than extrapolated.

The growing use of stochastic models and their comparative benefits

In modern times, computational power is such that actuaries now simulate a multitude of financial outcomes using stochastic models. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in the inputs over time. Distributions of potential outcomes are derived from a large number of simulations (stochastic projections), which reflect the random variation in the input. Stochastic modeling builds volatility and variability (randomness) into the simulation and therefore provides a better representation of real life from more angles. The differences in the approaches are illustrated in Figure 1.

What does all of this have to do with active investment management?

The problem of accurately estimating the future performance of a portfolio or strategy is very similar to the insurance company needing an estimate of future solvency. Unlike the insurance industry, predicting future strategy performance still largely relies on extrapolation of the past—despite the ubiquitous industry-standard disclaimer. Many methods have been developed over time to improve the situation. Some of the most common methods include cross-validation, scenario testing, and Monte Carlo techniques. Each of these has its pros and cons.

Cross-validation is simply the process of splitting available market data into in-sample and out-of-sample segments. The in-sample is used for optimizing the strategy, and the out-of-sample is used for performance estimation.

The method is very quick and easy to apply and does provide an unbiased estimate of future performance. However, the method leads to a single path outcome and potentially a large sampling error. As mentioned before, the problem with this is that a singular historical path is insufficient to predict future outcomes. To make matters worse, the results depend on an arbitrary choice on how to split the data, and it is psychologically almost impossible not to “cheat.” In other words, if the result is not favorable, the strategy developer is left with the choice to abandon strategy development or reuse out-of-sample data, leading to bias.

Scenario testing is another common method of strategy performance estimation. This involves stress testing the strategy using several possible scenarios developed either using historical time periods as guides or contrived potential future “worst-case” scenarios.

When might scenario testing be used? As an example, the first ETF for the U.S. equity market was created in 1993, and it took several years to see widespread acceptance and significant trading volume. A developer of an ETF strategy may want to examine how the strategy might have performed during the 1987 stock market crash. Because actual market data doesn’t go back that far, a scenario is created that approximates what might have happened. The primary benefit is that multiple scenarios (outcomes) are available from which to draw conclusions. However, the number of scenarios is limited both by historical context and the built-in biases of the person creating the scenarios. Each scenario can be time-consuming and tedious, which usually means the number of scenarios evaluated are limited.

A more advanced method involves the use of Monte Carlo techniques. This involves taking the historical returns of the strategy over time and randomizing the order and frequency in which they occur.

See Related Article: The case for mechanical trading strategies

The main advantage of the process is nearly infinite scenarios (outcomes) can be created through a relatively quick and easy process. The downside of this technique is that it uses a fixed set of predetermined trades, which might have been overfit (“overoptimized”) or just got lucky for a period of time. Additionally, the technique assumes that certain statistical preconditions are met, including the fact that any trade could have occurred in any order irrespective of volatility regime or money-management constraints. Many times these are not safe assumptions.

Stochastic models: A better way?

Just as in the insurance example, there is a better way. It is possible to more realistically estimate active strategy future performance using stochastic modeling. Figure 2 compares the stochastic approach as applied to active strategies with a deterministic approach.

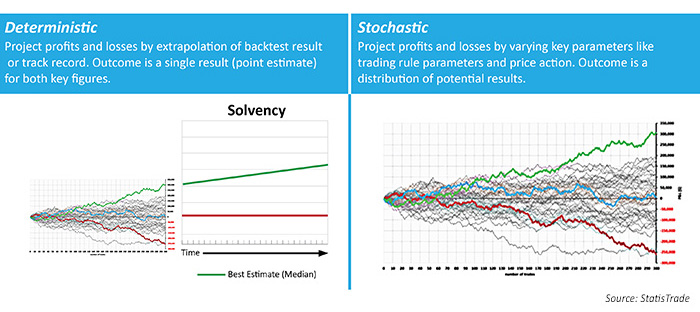
Although the basic idea behind the process when applied to an active strategy is the same as the insurance application, the mechanics of applying it are quite different. Unlike the insurance company example, general statistical approximations are not sufficient for some inputs. Specifically, price action can be critically important, as trading logic targets specific patterns in historical data. Instead of varying inputs (such as interest rates, equity returns, mortality rates, and default rates in the insurance case), the active strategy version inputs (such as price action, trading logic, investor behavior, corporate actions, and broker/exchange actions) are varied.

When properly applied, stochastic modeling simulates future real-life performance scenarios. Rather than using an extrapolation of the past, the method independently creates a multitude of scenarios using historical data as a guide. Stochastic models do not reuse historical trades nor make any assumptions on trade ordering and money-management constraints. All of these are realistically simulated in the model. The challenge of the approach is the complexity of implementation and experience needed to interpret results. In the insurance industry, there are teams of actuaries that develop and interpret stochastic models, so these challenges are not trivial.

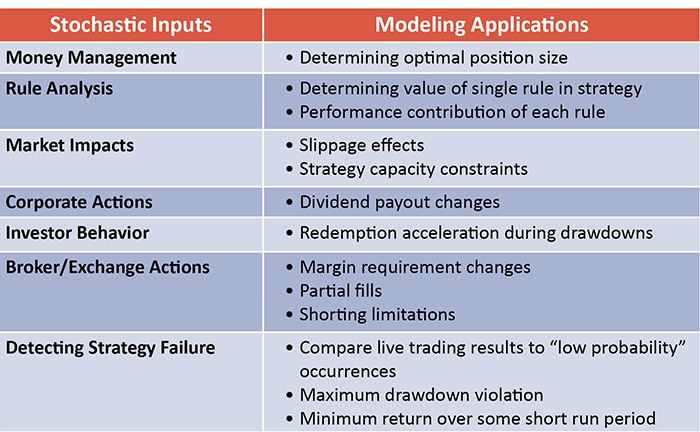
When properly applied, stochastic models not only realistically estimate future performance of an active strategy but also answer many more questions about what may be experienced by the practitioner. A sampling of these is shown in Table 1.

This discussion had covered several methods used to set expectations on future strategy performance. Many rely on extrapolation or reordering of the past, similar to how insurance companies used to forecast solvency before the computer age. With the advances in readily available computing power, the insurance industry has largely moved on to the better approach known as stochastic modeling. It is our belief that developers and practitioners of active investment strategies would benefit from examining the benefits of stochastic modeling. When the stochastic modeling methodology is applied correctly, more accurate performance forecasting for active strategies is possible.